Introducción

La enfermedad pulmonar obstructiva crónica (EPOC) es un trastorno permanente y progresivo que se caracteriza por la disminución del flujo en las vías aéreas y que está causado, principalmente, por una reacción inflamatoria frente al humo del tabaco1. Según la Organización Mundial de la Salud, todos los años la EPOC provoca la muerte de unos 3 millones de personas en el mundo. En España se estima que cada año mueren más de 18.000 personas por EPOC, que es la quinta causa de fallecimiento más común entre los varones, con una tasa anual de 55 muertes por 100.000 habitantes, y la séptima para las mujeres, con una tasa anual de 18 muertes por 100.000 habitantes2. Se estima que para el año 2020 la EPOC será la tercera causa mundial de defunción.

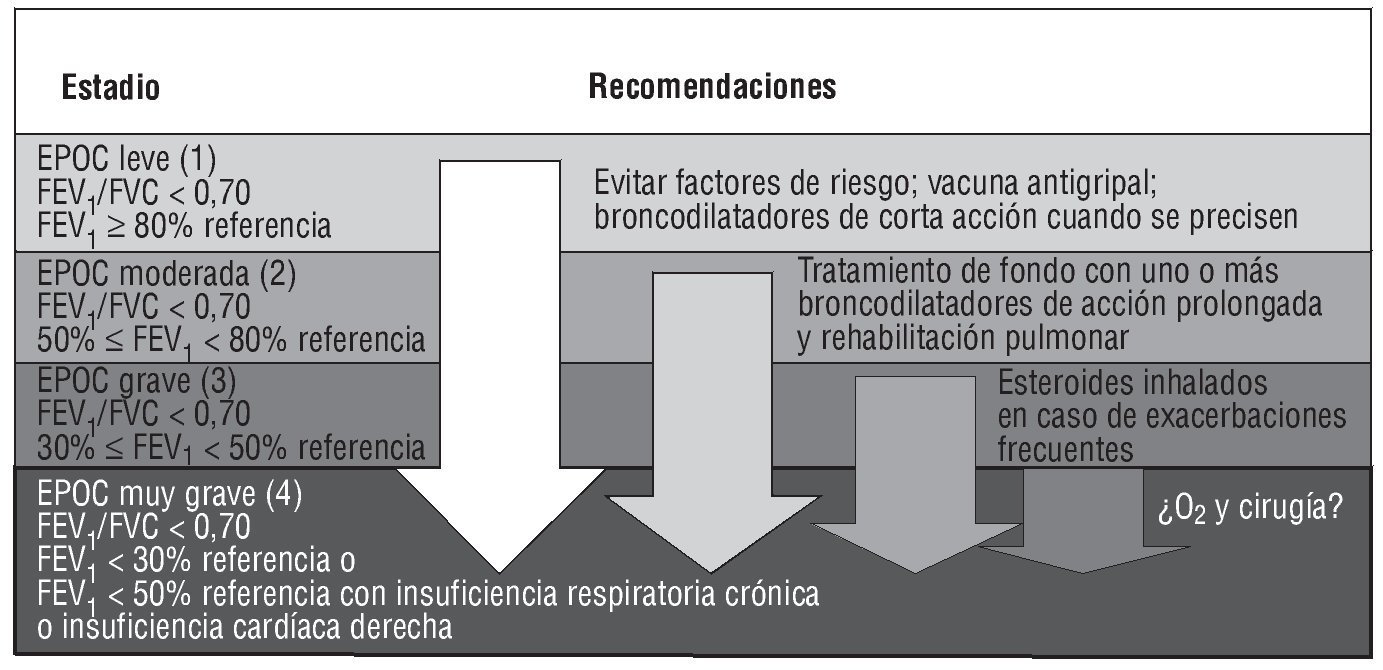
Para diagnosticar la EPOC es preciso realizar una espirometría, en condiciones basales y tras la inhalación de un agente broncodilatador, que muestre un valor del cociente FEV1/FVC menor de 0,70. La medida de la obstrucción al flujo aéreo (FEV1), expresada en porcentaje respecto al valor de referencia, es el mejor indicador de la progresión y la gravedad de la enfermedad. La Global Initiative for Chronic Obstructive Lung Disease (GOLD), en su edición de 2007, ha propuesto una clasificación de la gravedad de la EPOC en 4 estadios en función de los valores de la espirometría tras broncodilatación3 (fig. 1). A medida que la enfermedad progresa, la mayor gravedad de la obstrucción al flujo aéreo se asocia con más síntomas, peor calidad de vida y una mayor incidencia de exacerbaciones. La mayoría de los tratamientos existentes para la EPOC son sintomáticos y no han mostrado tener un efecto claro en la progresión y mortalidad de la enfermedad, probablemente debido al hecho de que la EPOC es un proceso heterogéneo de muy larga duración, con una gran variedad de fenotipos de pacientes, de situaciones clínicas y de evolución de la enfermedad.

Fig. 1. Criterios de Global Initiative for Chronic Obstructive Lung Disease (GOLD) para clasificar los estadios de la enfermedad pulmonar obstructiva crónica (EPOC). FEV1: volumen espiratorio máximo en el primer segundo; FVC: capacidad vital forzada; insuficiencia respiratoria crónica: presión parcial de oxígeno arterial (PaO2) < 60 mmHg (8,0 kPa) con o sin presión parcial de CO2 arterial (PaCO2) > 50 mmHg (6,7 kPa), respirando aire ambiente y al nivel del mar.

En los últimos años el número de estudios sobre la progresión y mortalidad en la EPOC ha crecido de manera muy significativa. Sin embargo, ciertos factores metodológicos asociados a este tipo de estudios han influido en sus conclusiones. Además, el análisis de la progresión y de la tasa de mortalidad suele llevar asociada la necesidad de un largo seguimiento y un alto número de participantes, lo cual limita especialmente la financiación y el seguimiento de este tipo de estudios.

Uno de los principales retos a la hora de estudiar la progresión de la enfermedad es definir los parámetros indicadores de dicha progresión. Históricamente, el descenso anual del valor del FEV1 ha sido el parámetro más utilizado a la hora de establecer la progresión de la EPOC. Mientras que en una persona sana este descenso anual suele ser de 20-30 ml, en pacientes con EPOC4 la media se encuentra en 60 ml. No obstante, se trata de un parámetro vinculado al estado de la función pulmonar y recientemente se ha cuestionado su correspondencia con la evolución fisiopatológica de la enfermedad5-7.

En el caso de los estudios de mortalidad asociada a la EPOC, las dificultades que entraña reconocer la causa específica de la muerte e identificar factores pronósticos de mortalidad de la enfermedad son los principales factores metodológicos que limitan la posibilidad de conseguir datos concluyentes. En cuanto a la dificultad a la hora de asignar la causa específica de muerte, diversos estudios han mostrado que la EPOC está infradiagnosticada y que en más de la mitad de los pacientes con EPOC muy grave ésta no aparecía en el certificado de defunción8.

El estudio TORCH9 fue el primer estudio internacional cuyo objetivo principal fue analizar todas las causas de mortalidad, así como las causas específicas relacionadas con la EPOC, en pacientes con EPOC moderada y grave. Las causas de muerte fueron analizadas por un comité independiente formado por 3 expertos, que obtuvieron una coincidencia del 83% en la adjudicación de la causa de muerte de los casos asignados y un 52% de coincidencia con la causa descrita en las historias médicas de los pacientes.

Con el propósito de encontrar factores pronósticos de mortalidad en pacientes con EPOC, se ha estudiado la asociación entre varios parámetros de esta enfermedad y la tasa de mortalidad. En un estudio epidemiológico, de 3 años de seguimiento, se describió una mortalidad de un 23% y la edad y el valor inicial del FEV1 antes de la administración del broncodilatador fueron factores pronósticos de la enfermedad. Además, tras ajustar el riesgo a la edad y al valor de FEV1, la mortalidad se relacionó positivamente con la capacidad pulmonar total y la frecuencia cardíaca, y negativamente con la tolerancia al ejercicio10. Otro estudio, que incluía a una cohorte de 5.542 personas seleccionadas de la población general, tras 22 años de seguimiento demostró que los pacientes con EPOC moderada o grave según la clasificación GOLD presentaban una supervivencia inversamente relacionada con el valor del FEV1 que tenían al entrar en el estudio (razón de riesgo relativo de 1,4 a 2,0 para la EPOC moderada y de 2,1 a 3,5 para la grave)11. Sin embargo, en un análisis prospectivo de 3 años de seguimiento en pacientes con EPOC hospitalizados con exacerbaciones agudas, se determinó una asociación positiva entre mortalidad y duración de la enfermedad (riesgo relativo [RR] = 1,158), valores bajos de albúmina (RR = 0,411) y un índice de masa corporal bajo (RR = 0,830), mientras que los valores del FEV1 no mostraban una asociación significativa12. También se ha descrito que hasta que el FEV1 es inferior al 50% del valor teórico, este parámetro no es un buen predictor de la mortalidad. De igual forma, en pacientes con FEV1 muy bajo esta medida tenía poco valor predictivo10.

Otro parámetro fisiológico que se ha considerado factor pronóstico de la EPOC es la capacidad inspiratoria (IC). Se ha descrito que la relación entre la IC y la capacidad pulmonar total (IC/TLC) podría ser una variable pronóstica de la evolución de la enfermedad, debido a su relación inversa con la mortalidad. En una cohorte de 689 pacientes con EPOC, con un 27% de fallecimientos durante los 5 años de seguimiento, se determinó que había una relación directa entre mortalidad y mayor edad, menor índice de masa corporal, menor tolerancia al ejercicio, más disnea y mayor relación IC/TLC. Tras realizar un análisis multivariante, el índice IC/TLC resultó un buen factor de mortalidad en pacientes con EPOC, independiente de otras variables13.

Otra razón que podría explicar la falta de datos concluyentes sobre la asociación entre los parámetros de función pulmonar y la mortalidad de la enfermedad en pacientes con EPOC es que ésta se asocia a importantes consecuencias sistémicas, tales como inflamación, desnutrición y debilidad muscular, lo que podría contribuir a la aparición de síntomas y a la morbimortalidad de la EPOC, sobre todo en sus fases avanzadas. Así, la categorización de los pacientes con EPOC en función del grado de disnea es más predictiva de supervivencia a los 5 años que la categorización según el FEV114. El peso corporal15,16, la capacidad para realizar ejercicio y la percepción del estado de salud, medida por cuestionarios de calidad de vida, son igualmente parámetros que han mostrado una asociación con la mortalidad en la EPOC17-20.

Diseño del estudio

Dada la naturaleza de las hipótesis en cuestión y de las dudas planteadas por los estudios ya realizados, es muy poco probable que nuevos estudios transversales y/o de casos y controles proporcionen más luces que sombras. Así pues, en la actualidad sólo se contemplan 2 opciones: los diseños de cohortes y los ensayos clínicos aleatorizados (ECA).

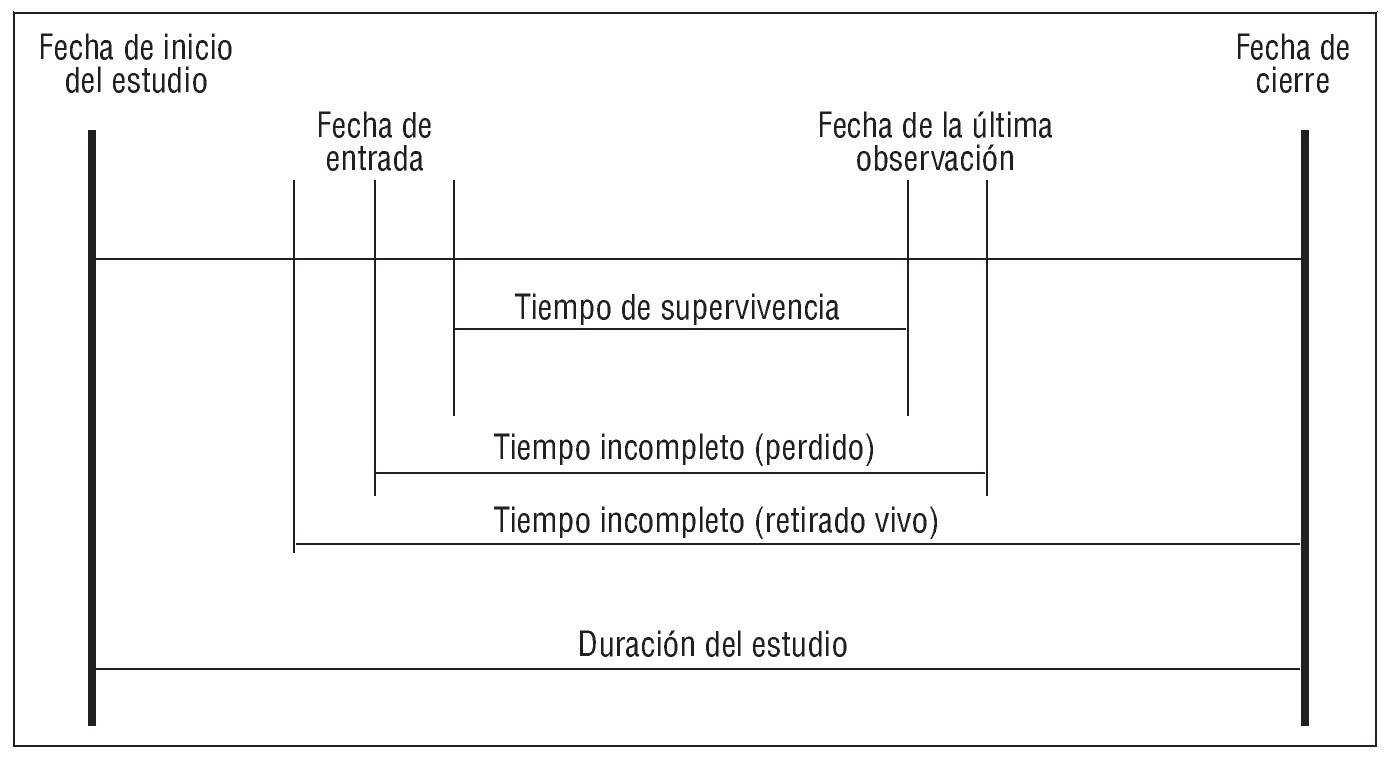
En esencia, el esquema general para ambos tipos de investigación es el mismo (fig. 2); esto es, entre las fechas de inicio y cierre del estudio se observan ciertas características de una muestra de efectivos que se incluyen, en general, de forma no simultánea, durante períodos diversos, dado que habrá un contingente de pacientes supervivientes al cierre del estudio, un segundo grupo que habrá fallecido durante el período de observación y un tercero que habrá abandonado antes de finalizar dicho período. La principal diferencia, que no única, entre ambos diseños reside en que el estudio de cohortes es observacional y el investigador no interviene en la asignación de individuos expuestos al factor en estudio (tratamiento farmacológico o no), mientras que en un ECA el investigador asigna la exposición al factor en estudio de forma aleatorizada y, cuando es posible, a doble ciego. De ahí se deriva la principal limitación de los diseños observacionales puros: ¿hasta qué punto los pacientes tratados son comparables a los que no han recibido tratamiento? ¿Cuál es el impacto del efecto placebo? Además, si la cohorte es retrospectiva, también será necesario resolver otras cuestiones metodológicas relevantes que guardan relación con la calidad y disponibilidad de los datos previamente registrados, y con los eventuales cambios en las definiciones de las variables (criterios diagnósticos, técnicas quirúrgicas o de laboratorio, tratamientos farmacológicos, etc.).

Fig. 2. Esquema general de los estudios.

Sin duda el ECA es el diseño que mejor resuelve los problemas de validez interna, puesto que la intervención del investigador optimiza la comparabilidad de los pacientes incluidos en cada grupo. No obstante, aun realizados mediante protocolos de investigación impecables, tampoco están exentos de problemas de validez. En efecto, el hecho de que la tasa de abandonos sea elevada y significativamente distinta en cada grupo9,21,22 condiciona la validez interna, y tanto la autoselección de los pacientes participantes, necesariamente voluntaria, como los criterios de inclusión y exclusión apropiados para evitar factores de confusión en la medida del efecto alejan las características de la muestra analizada de la población de referencia; esto es, en el caso de la EPOC, los pacientes atendidos en la práctica clínica habitual.

Variables de medida del efecto

La primera cualidad que debe poseer cualquier variable es la de medir con la máxima exactitud y precisión el fenómeno que representa y, como es lógico, sea cual fuere el tipo de estudio, las variables incluidas en los cuadernos de recogida de datos deben obedecer a definiciones precisas. Las investigaciones más recientes sobre la EPOC miden la evolución de la enfermedad mediante pruebas espirométricas, la frecuencia y la gravedad de las exacerbaciones, y el deterioro del estado de salud y la calidad de vida de los pacientes.

Los criterios GOLD3, cuyo esquema se reproduce en la figura 1, se han utilizado para clasificar el grado de progresión de la EPOC en investigaciones recientes. Sin embargo, este parámetro muestra una desviación estándar muy grande6,7,23. Otra limitación que presenta el uso del descenso anual del FEV1 como indicador de progresión de la EPOC es que la espirometría plantea problemas en cuanto a la calibración de los aparatos y la competencia y homogeneidad de los investigadores respecto a la técnica, el procedimiento y las condiciones de realización de la prueba, problemas que suelen paliarse mediante la formación específica y el uso del mismo modelo de instrumento, algo de especial dificultad en estudios multicéntricos y/o internacionales.

Otros parámetros propuestos como indicadores de progresión de la enfermedad son la disminución de la capacidad de realizar ejercicio, que es el resultado de la combinación de la disminución de la función pulmonar y los efectos extrapulmonares de la EPOC (problemas cardiovasculares y debilidad muscular)24; la disminución de la calidad de vida25 y la utilización de los recursos sanitarios26,27. Estos parámetros también llevan asociadas importantes dificultades por lo que respecta a su empleo en estudios de larga duración y/o con un alto número de individuos. La frecuencia de las exacerbaciones también se ha utilizado para medir la progresión de la EPOC. Sin embargo, existen diversos problemas metodológicos asociados, como la variabilidad en la definición y la adjudicación de exacerbación28, la dependencia de la situación basal del paciente29 y la variabilidad en la medicación previa administrada a cada individuo28,30, por lo que es necesario conocer en detalle las definiciones empleadas para interpretar correctamente los resultados de una investigación. Asimismo, la intervención de comités de expertos que supervisen de forma centralizada los criterios efectivamente utilizados por los investigadores clínicos es una fórmula acertada para mejorar la calidad de esta variable.

Recientemente se ha publicado la validación del modelo BODE como predictor de exacerbaciones, hospitalizaciones y mortalidad en la EPOC31,32. Este índice incorpora 4 parámetros: función pulmonar (FEV1), síntomas (disnea), capacidad de ejercicio (prueba de la marcha) y estado nutricional (índice de masa corporal), lo que apoya la necesidad de una evaluación multidimensional de la EPOC. Este concepto permitirá un mejor conocimiento y manejo de la EPOC, así como el desarrollo de nuevos tratamientos combinados que actúen sobre todos los elementos implicados tanto en las manifestaciones pulmonares como en las sistémicas de esta enfermedad.

Puhan et al33 mostraron que los cuestionarios específicos, como el St. George's Respiratory Questionnaire, proporcionan medidas más sensibles y específicas del estado de salud y la calidad de vida de los pacientes con EPOC que los cuestionarios generales como es el SF-36, que tiene en el SF-12 una versión reducida. Se trata de una variable de gran interés, dado que la EPOC afecta progresivamente y de forma importante el bienestar del paciente.

Representatividad de la muestra

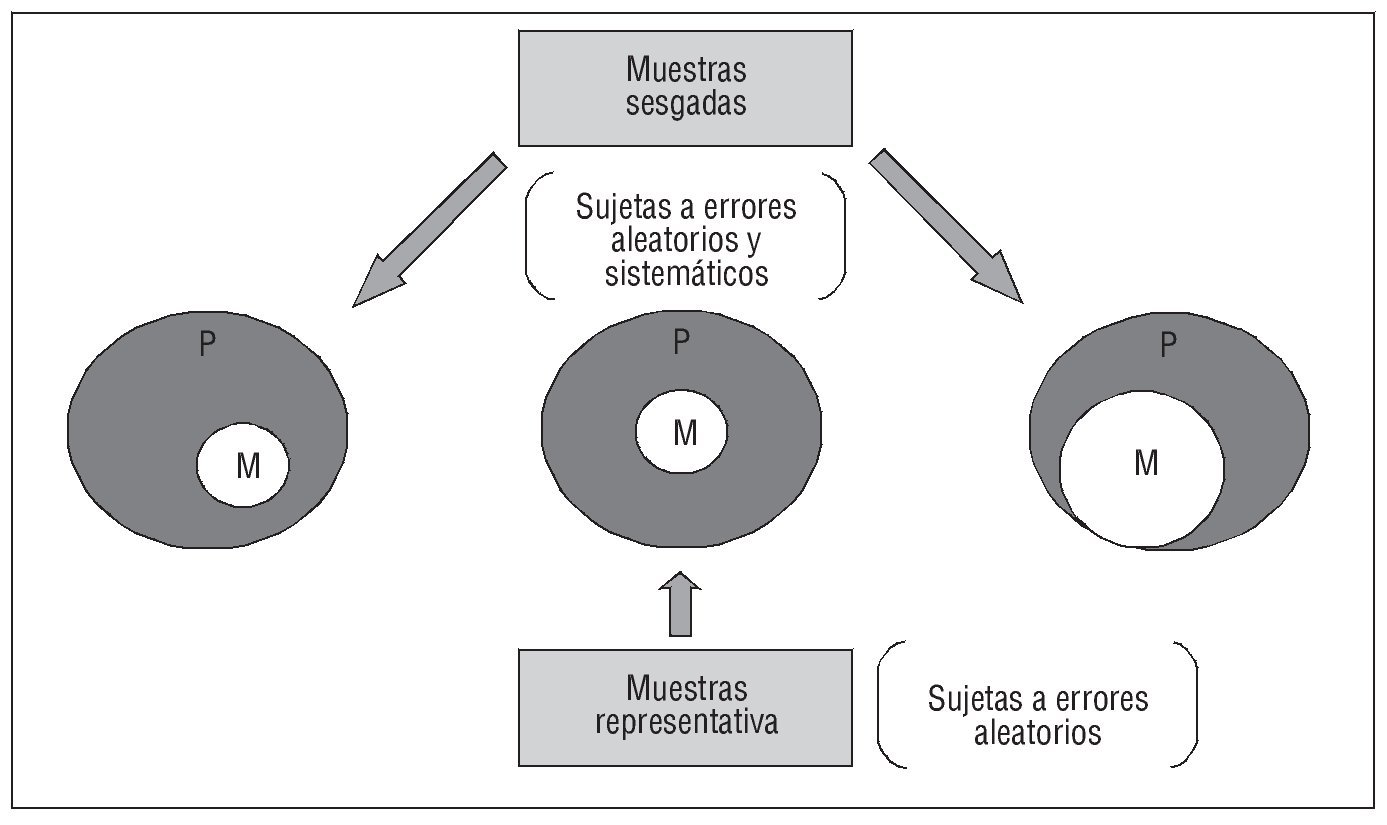
Conviene recordar que la representatividad o exactitud de una muestra nada tiene que ver con su tamaño ni con su precisión; es decir, tal como ilustra la figura 3, una muestra puede ser grande y sesgada, pequeña y representativa, o cualquier otra combinación de ambos atributos. De acuerdo con la teoría de muestreo, la representatividad de una muestra depende de que todos los componentes de la población diana hayan gozado de igual probabilidad de formar parte de la muestra efectivamente seleccionada. Así, el único método que garantiza la igualdad de probabilidad exigida es el aleatorio simple, que, sin embargo, suele presentar problemas de aplicación insalvables en la investigación clínica y epidemiológica. Por ello comúnmente se recurre a procedimientos de selección seudoaleatorios -que se aproximen, cuanto más mejor, a los aleatorios-, definidos a partir de ciertos criterios de inclusión y de exclusión, concebidos para sustentar razonablemente la comparabilidad entre grupos (validez interna) y la generalización de los resultados (validez externa): 2 centros de interés que, por otra parte, colisionan con frecuencia. Basta revisar los criterios de exclusión de ECA recientes9,22 para comprobar que, en legítimo interés de la validez interna, estos estudios excluyen a sujetos que forman parte de los pacientes tratados en la práctica clínica habitual, lo que, sumado al inevitable proceso de auto-selección de voluntarios, implica que los resultados de los ECA pueden no reproducirse exactamente en la práctica clínica; tanto más cuanto los criterios de inclusión no son los mismos en todos los estudios y, por consiguiente, sus conclusiones no son generalizables a poblaciones de referencia idénticas.

Fig. 3. Representatividad o exactitud de una muestra.

También debe tenerse en cuenta la posibilidad de incurrir en el sesgo de Berkson, descrito en 1946 a partir de la observación de una asociación negativa entre el cáncer y la tuberculosis pulmonar. Consiste en un sesgo de selección que puede darse cuando -como suele ser el caso- los pacientes investigados son seleccionados en centros hospitalarios bien sea para un ECA o un estudio de cohortes. Se deriva del hecho circunstancial de que la exposición a alguno de los factores de riesgo del estudio -léase tabaquismo o tratamiento esteroideo- aumenta la probabilidad de enfermar en general y, en particular, de ingresar en un hospital, en cuyo caso la tasa de exposición en el grupo control podría estar sobrestimada. Obsérvese en este sentido que los estimadores obtenidos en muestras sesgadas están sistemáticamente desviados en una u otra dirección y que, por lo tanto, son inexactos y pueden -aunque no necesariamente- inducir a conclusiones falaces, salvo que el sesgo se haya identificado, medido y corregido.

Tamaño muestral

El número de efectivos estudiados determina la precisión de los estimadores y de los tests de hipótesis estadísticas. Respecto a estos últimos, la precisión se mide mediante la probabilidad de error que se asume en caso de rechazarse la hipótesis nula o de no asociación (error alfa o de tipo I), y la probabilidad de error que implica aceptar la hipótesis nula (error beta o de tipo II), con frecuencia indicado en forma de potencia estadística (1 - beta) expresada en porcentaje. Así, se trata de errores aleatorios que disminuyen conforme se aumenta el tamaño muestral. Nótese, no obstante, que su reducción no tiene ningún efecto en eventuales sesgos, y que alfa y beta no son probabilidades complementarias -esto es, no tienen por qué sumar la unidad-; por consiguiente, es posible que, en contrastes dados, la inferencia estadística no permita ni afirmar ni negar la hipótesis nula asumiendo probabilidades de error suficientemente pequeñas para ambos enunciados.

Limitaciones presupuestarias aparte, el tamaño muestral idóneo para una precisión dada depende de la incidencia de las variables dependientes (a menor tasa, mayor número de efectivos), de la diferencia que se quiera observar entre grupos (a menor diferencia, mayor muestra) y de la proporción esperada de pérdidas y abandonos. Sobre este punto se destaca que la precisión de un estudio se calcula a partir de los datos efectivamente observados, con independencia de las estimaciones realizadas en el protocolo de la investigación -con frecuencia, optimistas.

Duración del estudio

Para estudiar adecuadamente la progresión de la enfermedad y la supervivencia en pacientes con EPOC, el sentido común apunta que no es posible analizar un fenómeno si no se observa en su conjunto. Por consiguiente, los períodos de observación deberían extenderse tanto como dura la historia natural de la enfermedad desde su inicio hasta la defunción del paciente. Sin embargo, llevar a cabo una investigación que cumpla con este requisito implica costes muy elevados, dificultades logísticas de primera magnitud y, en el caso de los ECA, acaso limitaciones éticas insoslayables. No sorprende, pues, que los ECA recientes y en curso limiten su duración a 222, 39 y 4 años21. Con todo, estos períodos de investigación dejan una cuestión en el aire: ¿el comportamiento de los supervivientes después de cerrar el estudio será semejante al observado?

Por otra parte, aumentar el tamaño de la muestra no resuelve este problema, aunque pueda disimularlo. Lo cierto es que acumular, por ejemplo, 6.000 años-persona mediante 1.000 pacientes seguidos durante 6 años o con 6.000 pacientes seguidos durante un año proporciona la misma precisión estadística, a pesar de no significar científicamente ni mucho menos lo mismo.

Pérdida de efectivos

Es el problema logístico por excelencia de los estudios prospectivos en general, que arrecia cuanto mayor es el período de seguimiento y que conlleva 2 consecuencias secundarias de primer orden: disminución de la precisión preestablecida cuando las pérdidas son mayores que las pronosticadas, e introducción de sesgos cuando las causas de las retiradas no son independientes del efecto que se desea observar.

Los datos correspondientes a los efectivos que han abandonado un estudio pueden tratarse de diversas maneras; por cierto, ninguna satisfactoria. Hacer caso omiso de ellos es una solución hoy en desuso, dado que procediendo así no se tiene en cuenta que los sujetos retirados han sobrevivido hasta la fecha del abandono; en consecuencia, el riesgo se sobrestimará. Por el contrario, dar por supuesto que han sobrevivido -otra solución felizmente en desuso- implica subestimar el riesgo. Asimismo, considerar que su comportamiento habrá sido semejante a los observados también es una opción escasamente sustentable, puesto que conlleva aceptar a ciegas hipótesis indisociables de las que se pretende contrastar.

En la actualidad, el tratamiento común que reciben los datos de los abandonos es considerarlos censurados, lo que se traduce en dar por supuesto que las causas de las retiradas no están relacionados con la enfermedad; es decir, que la probabilidad de abandono es independiente del riesgo investigado, lo que tampoco está exento de controversia, ya que de hecho es posible que la decisión de abandonar sea consecuencia del empeoramiento del estado físico, de un cambio de residencia en busca de un clima mejor o de un cambio en la actividad laboral al objeto de evitar -si es el caso- el factor de riesgo en estudio. En este sentido, es claro que el valor veritativo de los resultados de los estudios INSPIRE (un 38,6% de abandonos) y TORCH (un 39,1%) está fuertemente condicionado por la conformidad de la hipótesis subyacente a la censura de los datos, tanto más cuanto en ambos ensayos se han observado mayores pérdidas en el grupo placebo9.

No hay una solución ideal para el tratamiento de la pérdida de efectivos, salvo que se produzcan en una proporción lo suficientemente pequeña para no sesgar los resultados de la investigación sea cual fuera su destino real. Por ello, incorporar a los proyectos de investigación de larga duración programas de motivación e incentivación dirigidos a pacientes, y/o acciones complementarias de rastreo y localización de submuestras de casos perdidos se vislumbran como fórmulas adecuadas para paliar el impacto de este problema21.

Análisis estadístico

El conjunto de técnicas estadísticas que se emplean para analizar la progresión de la enfermedad en pacientes con EPOC son las que se conocen generalmente como "análisis de supervivencia". El término "supervivencia" se debe a que en un principio estos métodos se concibieron para estudiar el tiempo hasta la muerte de un paciente (fundamentalmente en el campo de la oncología).

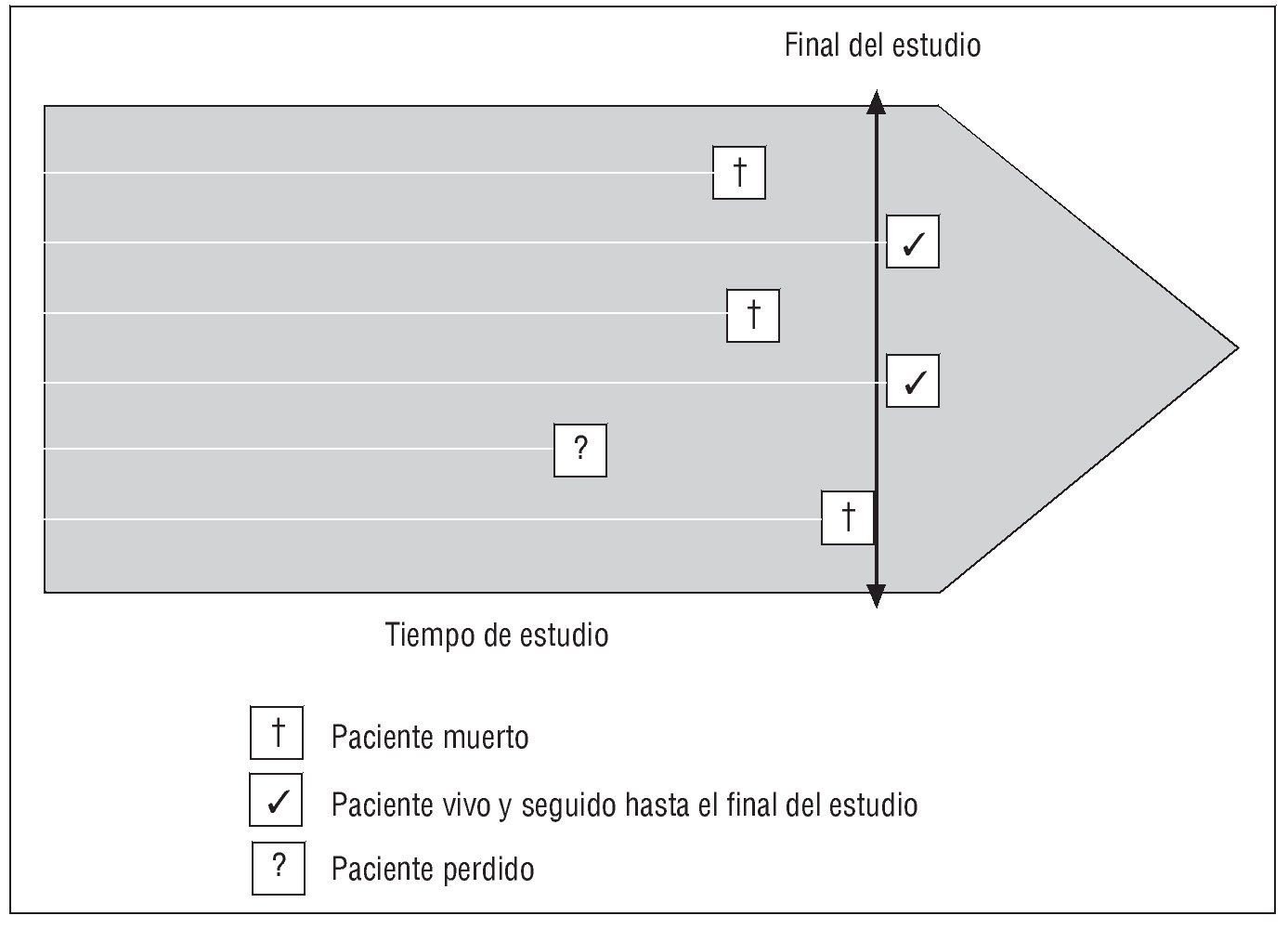
Este método permite estudiar la variable "tiempo transcurrido hasta que se produce un evento" y su dependencia de otras posibles variables explicativas. La variable respuesta no es un valor numérico único, como podría ser la presión arterial, sino que toma la forma de "tiempo transcurrido hasta un suceso" (time-to-event) y contempla la combinación de 2 elementos: si se ha producido o no el suceso (muerte, recidiva, aparición de síntomas, etc.) y cuánto tiempo ha tardado en llegarse al desenlace, por lo que el seguimiento viene definido por una fecha de inicio y una fecha de cierre que lo determinan. La característica más importante de este tipo de datos (tiempo hasta que ocurre un suceso) es que, muy probablemente, al final del período de observación no todos los pacientes habrán presentado el suceso o evento objeto del estudio. Además, puede ocurrir que algunos pacientes se hayan perdido por causas diversas, sin que haya sido posible determinar su estado al final del período de observación. Cuando el suceso es la muerte, el individuo puede haber fallecido por causas diferentes de las que se analizan (p. ej., un accidente). Además, es habitual que los pacientes vayan incorporándose durante todo el período de observación, con fechas de inicio y cierre diferentes para cada uno, por lo que la probabilidad de que ocurra el suceso es menor en las últimas incorporaciones. Cuando los tiempos de supervivencia no se conocen con exactitud, es decir, las observaciones se presentan incompletas, los casos se consideran censurados (fig. 4).

Fig. 4. Tipología de los datos obtenidos.

Aunque se llame "análisis de supervivencia", no siempre tiene que ser la defunción el acontecimiento de desenlace, pero siempre debe tratarse de acontecimientos que, como la muerte, sean irreversibles. El análisis de supervivencia recogerá si se ha producido o no el suceso y el tiempo (en años) desde que cada paciente se incorporó al estudio hasta que murió o se produjo el evento; en caso de que no muera o no se produzca el suceso, se indicarán los años totales de observación. La variable tiempo es una variable continua y no normal, generalmente de distribución asimétrica.

En este tipo de análisis son necesarios ciertos requisitos: definir con exactitud el origen o inicio del seguimiento, definir la escala del tiempo y definir apropiadamente el evento. Además, en este tipo de análisis se asume un supuesto básico -que no siempre se da- y es que los pacientes no censurados representen bien a los censurados.

El análisis puede realizarse mediante técnicas paramétricas y no paramétricas, siendo estas últimas las más utilizadas debido a la naturaleza casi siempre no gaussiana de los datos a analizar.

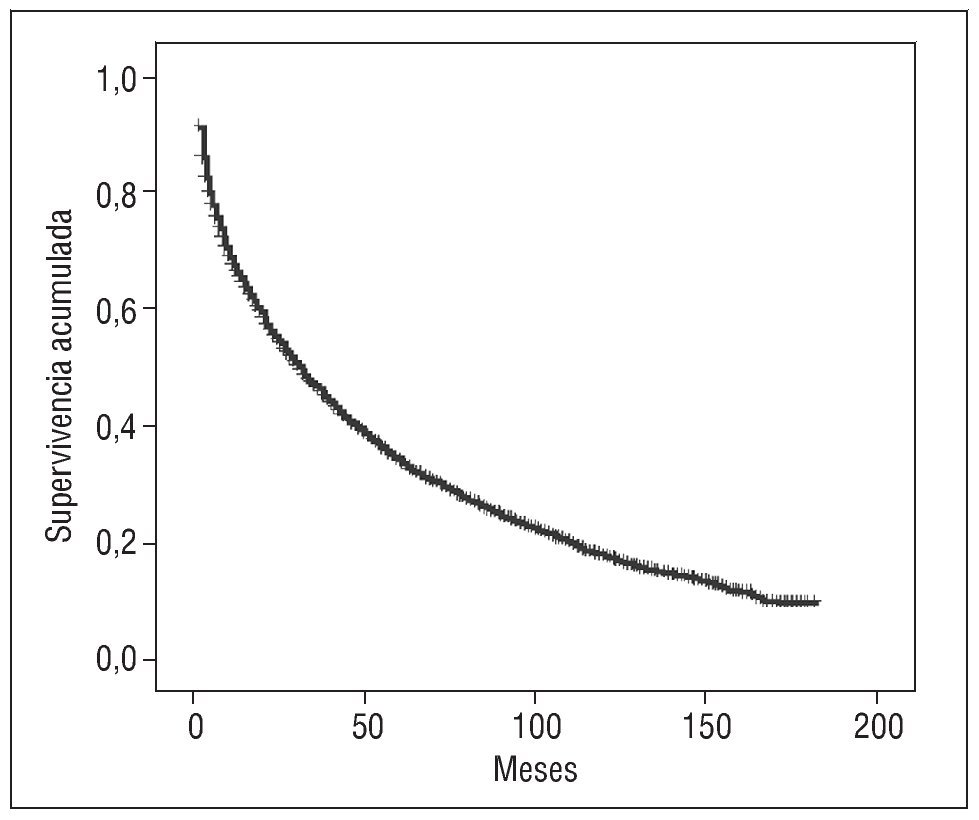
Para calcular la probabilidad de supervivencia individual acumulada a lo largo del tiempo suele utilizarse el método de Kaplan-Meier34, un método no paramétrico que no asume que los datos tengan una distribución particular y asume que los sujetos censurados se habrían comportado del mismo modo que los que han sido seguidos hasta el evento. Para describir la supervivencia por este método hay que disponer del tiempo durante el cual se ha observado al paciente y el estado del paciente al final del seguimiento. El método de cálculo empleado lo convierte en especialmente útil para estudios con un número pequeño de pacientes. En general, este análisis suele acompañarse de la respectiva representación gráfica, llamada curva de Kaplan-Meier (fig. 5), con el objetivo de expresar visualmente cómo va disminuyendo la probabilidad de sobrevivir a medida que pasa el tiempo. La curva debe interpretarse en su aspecto general, puesto que las conclusiones que se extraigan de los detalles particulares en diferentes puntos de aquélla no son fiables, sobre todo en los extremos, donde la estimación es menos precisa.

Fig. 5. Probabilidades de supervivencia en el tiempo.

En las ocasiones en que no se dispone de observaciones individuales de los eventos, sino de observaciones agrupadas por intervalos de tiempo (p. ej., los datos de mortalidad para un país), se utilizará el cálculo actuarial también conocido como método de Cutler-Ederer, en el que se divide el tiempo en intervalos y se calcula la supervivencia en cada uno de ellos. Este método implica 3 premisas: a) que todos los abandonos durante un intervalo dado ocurren aleatoriamente durante dicho intervalo; b) que la probabilidad de supervivencia en un tiempo dado es independiente de la probabilidad de supervivencia en los demás períodos, y c) que las personas que se retiran del estudio tienen un destino parecido a los que se quedan.

Para comparar 2 o más curvas de supervivencia de forma global se usan diversas pruebas estadísticas de contraste de hipótesis. La hipótesis nula que se contrasta es que los grupos comparados presentan igual supervivencia globalmente, esto es, que no hay diferencias persistentes. La prueba más empleada para comparar curvas de supervivencia es el test de rangos logarítmicos, también llamado test generalizado de Savage35,36, que tiene en cuenta las diferencias de supervivencia entre grupos en todos los puntos del tiempo que dura el seguimiento. Además de éste, hay otros tests de comparación de curvas de supervivencia: test generalizado de Wilcoxon (o test de Breslow), test de Tarone-Ware, test de Peto-Peto-Prentice y test de Fleming-Harrington. En general, se recomienda utilizar el test de rangos logarítmicos cuando el evento es poco frecuente o las curvas no se cruzan; en este caso, además, los resultados obtenidos del resto de tests serán similares37. Cuando las curvas se cruzan, se recomienda realizar al menos otro test de comparación, preferentemente el de Wilcoxon.

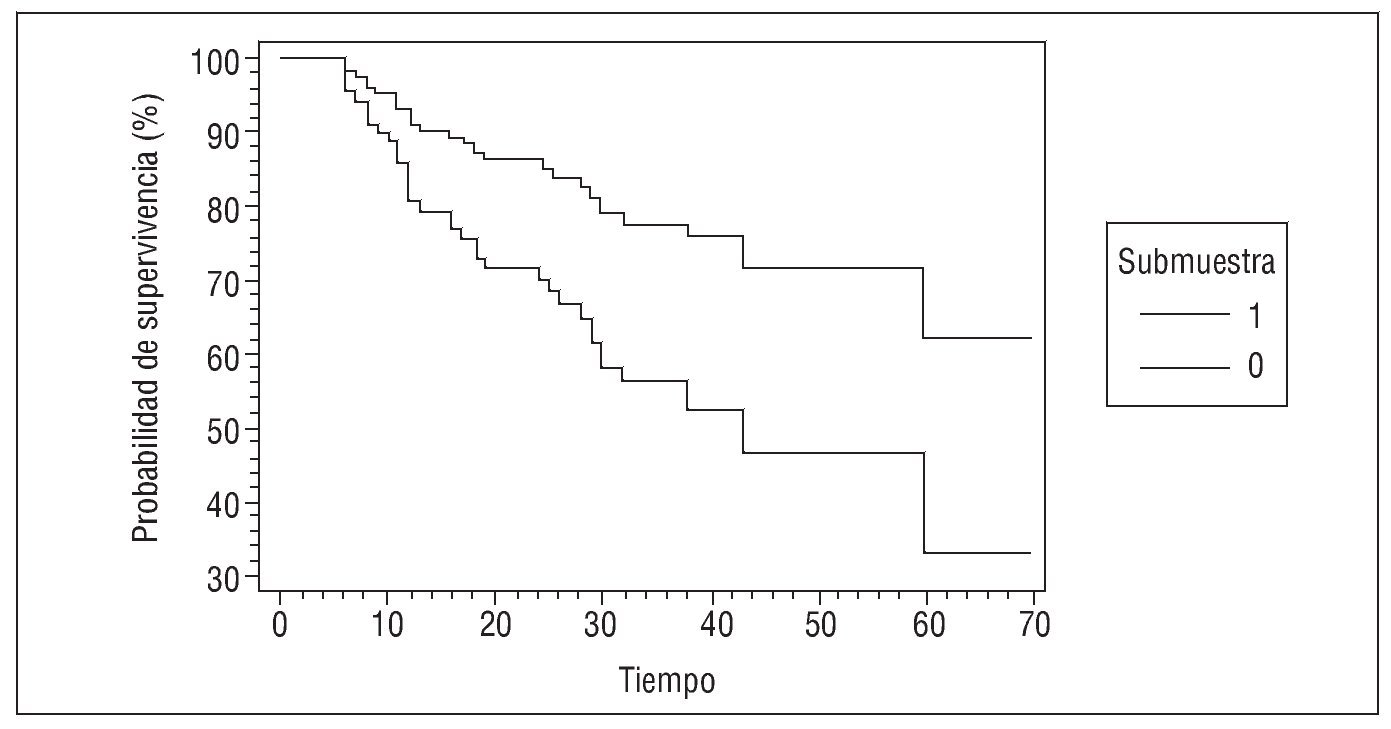
Si lo que se desea estudiar es si la variable dependiente está relacionada con la supervivencia de los individuos y conocer simultáneamente el efecto independiente de una serie de factores sobre esta supervivencia, se utilizará la regresión de Cox (modelo de riesgos proporcionales)38-40. Este método debe utilizarse cuando se estudie un suceso que sólo ocurra una vez como máximo, puesto que para sucesos o complicaciones que se repitan más de una vez en algunos pacientes durante el seguimiento debería recurrirse a la regresión de Poisson41. La regresión de Cox es la extensión multivariable del análisis de supervivencia y usa modelos próximos a la regresión logística (fig. 6). Esta técnica permite identificar y evaluar la relación entre un conjunto de variables explicativas y la tasa de aparición del suceso de interés, y predecir las probabilidades de supervivencia (o de permanencia sin el evento) para un determinado sujeto a partir del patrón de valores que presenten sus variables pronóstico. La regresión de Cox asume algunos de los mismos supuestos que el método de Kaplan-Meier: a) el suceso debe ser irreversible; b) debe poder ocurrir una sola vez, y c) la censura no debe ser informativa. En la interpretación de una regresión de Cox, el parámetro de asociación que se obtiene es una hazard ratio (razón de riesgo), que corresponde a una tasa instantánea, que conceptualmente sólo requiere una duración de tiempo infinitesimal para que ocurra el suceso. Así, el hazard a tiempo t es el cociente entre quienes mueren en ese tiempo y quienes estaban en riesgo de morir. El valor mínimo de la razón de riesgo es 0, el máximo infinito. El modelo de Cox promedia de manera ponderada las razones de riesgo de los diversos momentos en que se produce alguna muerte.

Fig. 6. Probabilidades de supervivencia estimadas según la regresión de Cox.

En el análisis de supervivencia también hay opciones paramétricas para la estimación de funciones de supervivencia y para la realización de contrastes de hipótesis sobre éstas. A tal efecto será necesario suponer ciertas funciones de probabilidad para la variable tiempo de espera y comprobarlas mediante ciertas pruebas de ajuste.

Algunas distribuciones paramétricas se han empleado repetidamente en la literatura médica para llevar a cabo análisis de supervivencia. Probablemente la distribución exponencial es la más simple de todas ellas. La característica más importante de esta distribución es que su función de riesgo se mantiene constante, caracterizando la exponencial como una distribución sin memoria de tiempo (un paciente tiene la misma probabilidad de morir en cualquier momento). La distribución de Weibull es una generalización de la exponencial que ha recibido una atención especial durante los últimos años debido a su simplicidad y flexibilidad42,43. Además de la exponencial, se han utilizado otras distribuciones como la lognormal, gamma, Rayleigh y Gompertz, aunque en menor medida44.

En cuanto a las limitaciones del análisis de supervivencia en estudios de EPOC, cabe destacar que en los últimos 5 años han aparecido varios estudios epidemiológicos de base poblacional que han señalado un posible impacto del tratamiento con corticoides inhalados en la mortalidad observada en pacientes con EPOC45, y cuyas conclusiones han suscitado varias críticas basadas fundamentalmente en el denominado "sesgo de tiempo in-mortal", referido a la ventaja que supone para el grupo de tratamiento la necesidad de que los pacientes incluidos en él tengan forzosamente que sobrevivir durante el período posterior a la inclusión y anterior al tratamiento. Este sesgo se superpone con el denominado de "tiempo variable", que hace referencia al hecho de que al computar el tiempo de supervivencia en ocasiones se incluyen períodos de no tratamiento. Ambos sesgos operan en la dirección de demostrar el efecto. Sin embargo, cabe destacar que pueden cuantificarse y, por lo tanto, corregirse.

Además del análisis de la supervivencia, hay otros resultados distintos de la mortalidad más difíciles de medir pero de gran importancia, como: estado funcional, calidad de vida, ausencia de dolor y otros síntomas, satisfacción con los cuidados médicos y calidad de la muerte. Todo ello es especialmente cierto para pacientes con enfermedades crónicas como la EPOC, para los cuales la calidad de vida puede ser de gran relevancia.

En los últimos años, en los estudios de coste-beneficio ha aparecido otro concepto que permite ponderar la supervivencia respecto a la calidad de vida: los años de vida ajustados por calidad. Éstos pueden ser útiles en este tipo de estudios, ya que permiten incorporar la calidad y la cantidad de vida ganada tras la aplicación de un procedimiento terapéutico por medio de sencillos métodos de cálculo.

Conclusiones

Diversas investigaciones llevadas a cabo recientemente arrojan ciertas dudas respecto a la eficacia del tratamiento farmacológico en la progresión y mortalidad de la EPOC, debidas, en primer lugar, a la débil significación estadística observada. No obstante, para valorar en su justa medida los resultados de dichos estudios también merecen consideración diversos problemas metodológicos, muchos de ellos derivados de la larga duración de la enfermedad y de las consiguientes dificultades que entraña el seguimiento de los pacientes.

De hecho, la elevada tasa de abandonos afecta con frecuencia la validez interna, tanto más cuando la distribución no es homogénea entre los grupos de intervención y de control. Asimismo, es preciso valorar el eventual efecto del sesgo de Berkson -derivado de incluir exclusivamente a pacientes hospitalarios-, corregir los sesgos de tiempo inmortal y de tiempo variable, y evitar el empleo de pruebas estadísticas basadas en distribuciones gaussianas.

Por otra parte, también conviene tener en cuenta que los rigurosos criterios de inclusión y de exclusión necesariamente empleados en los ECA para optimizar la comparabilidad entre los grupos investigados suelen restar representatividad a las muestras examinadas respecto a los pacientes atendidos en la práctica clínica habitual.

En suma, en el momento actual no se dispone de datos concluyentes. Por ello es necesario realizar nuevos ECA de mayor duración -tanta como sea posible- y con menores tasas de abandonos, al objeto de contrastar el efecto de los tratamientos farmacológicos en condiciones experimentales, sin que ello sea obstáculo para ampliar y completar a posteriori el conocimiento objetivo mediante la realización de estudios cuasi experimentales y/o de cohortes en poblaciones naturales.

Declaración de conflicto de intereses

Los autores han declarado no tener ningún conflicto de intereses.

Correspondencia:

Dr. J. Andrés Martínez.

GOC Networking. Josep Irla i Bosch, 5-7, 1.o. 08034 Barcelona. España.

Correo electrónico: andresmj@gocgrup.com