Current technological progress opens the door to measuring ever more biological processes and identifying bio-mechanism patterns at an unprecedented level of resolution. Faced with the ensuing avalanche of information, the promises of digital, precision and personalized medicine are increasingly fulfilled,1 and their success largely depends on the intensive use of data-driven approaches, particularly those stemming from the confluence of statistics and machine learning research. However, nowadays the application of statistics and machine learning in many modeling tasks, from specific risk injury prediction to general physiology,2 remains limited and constitutes a topic of great controversy that has divided experts about their ability to obtain useful results.3–7

A critical point which has gone largely unnoticed in the medicine field is the need to quantify the predictive limits of the models through uncertainty analysis. Practitioners and researchers tend to focus on performing inferential analysis to measure the uncertainty regarding the conditional mean (the expected value for a particular characteristic given that a certain set of conditions is known to occur), which presents important limited practical interpretations as the sample size grows.8 However, they usually ignore the conditional distribution, which is more informative in practice and helps to establish the reliability of the predictive results obtained from different sets of values for model inputs.

In our opinion, it would be advisable to provide, as the output of any predictive model, not only the point estimates, for example, of the conditional mean, but also a prediction band estimated by using the heteroscedastic signal of the predictive model. This prediction band is built as an estimate of the interval in which a future observation will fall, with a certain probability, given what has already been observed. We exemplify it from the results of our previous study on the submaximal prediction of maximal oxygen uptake in a general population.9 Following previous functional regression models,10 this time we quantify uncertainty using the conformal inference framework,11,12 which ensures to construct valid prediction bands with respect to the coverage error.13

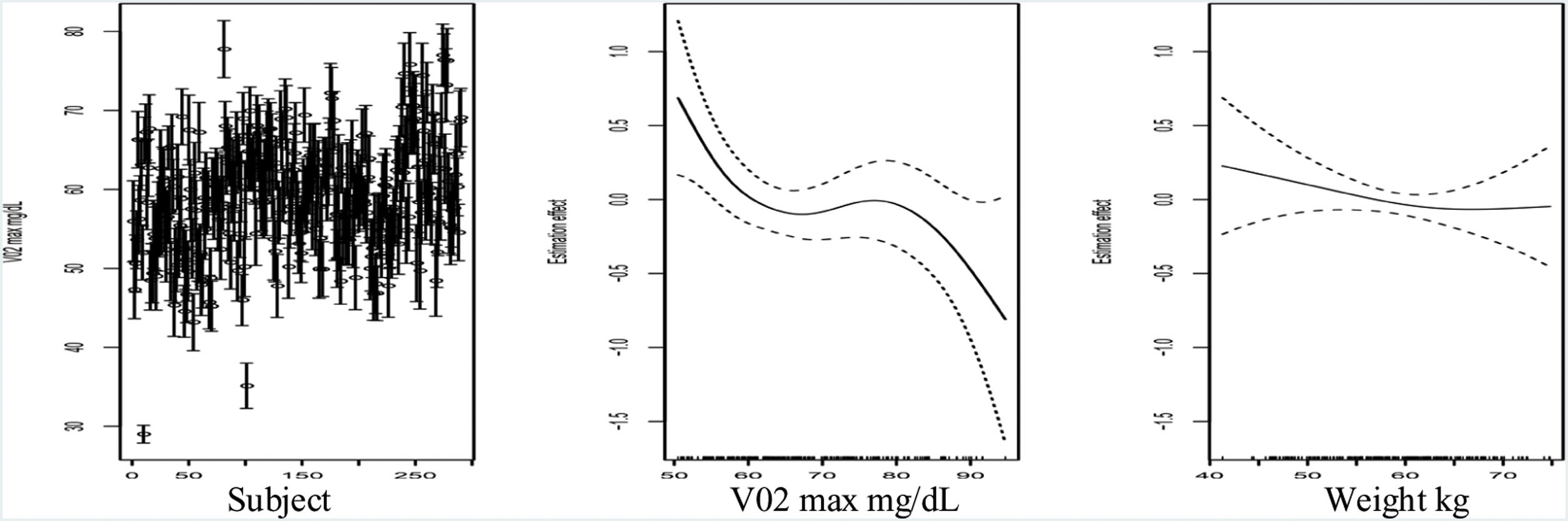
Fig. 1 (left) shows the prediction intervals for these individuals. In general, we observe a significant heterogeneity, indicating that the signal noise is heteroscedastic, and the uncertainty is high in the prediction results. This phenomenon happened despite the global predictive ability of the reported models, being reasonable in terms of the coefficient of determination (R2=0.80). In a more specific analysis, we try to predict with generalized additive models (GAM) the factors on which the radius of the prediction intervals depends. Let us recall that GAM is a generalized linear model in which the response variable depends linearly on unknown smooth functions of some predictor variables.14 After testing the linearity assumption, age is shown to exhibit a linear dependence, and with the increase of one year of age, the radius increases by 0.05, meaning that 40-year-old individuals versus 20-year-old individuals increase their radius in one point. In terms of peak oxygen (Fig. 1 (center)), we observe that when peak oxygen increases the uncertainty decreases, and a similar behavior can be observed when the weight increases (Fig. 1 (right)) in the range of 50–70kg. Importantly, the R2 of this model is equal to 0.16. According to this regression model, the uncertainty is heterogeneous and varies according to the level and physical conditions of the individuals. Ultimately, in those individuals with high-uncertainty values, the model's usefulness may be questioned.

Fig. 1.

(Left) Prediction interval of maximum peak oxygen with conformal inference techniques in all subjects. (Center) Additive effect of a GAM concerning oxygen consumption in the prediction of the radius of the prediction interval. (Right) Additive effect of a GAM concerning weight in the prediction of the radius of the prediction interval. Age, maximum peak oxygen and weight are statistically significant variables in the GAM model. Sex is not a statistically significant variable. The R-squared of the model is equal to 0.16. We use a linear link and a gaussian distribution as random error.

(0.14MB).

On the other hand, a closer inspection of the level of uncertainty in the prediction results can provide a crucial information for clinical management. As we have highlighted in a previous application in modeling five-year glucose changes in the general population, a phenotypically characterization of those subpopulations for which the model provides an unreliable prediction may be used to guide a specific approach, built on new assumptions, measurement procedures and interventions.1,2,9 Particularly, we showed that long-term changes in glycated hemoglobin cannot be adequately predicted for individuals with elevated fast plasma glucose (FPG) levels, and the same holds true for individuals with FPG levels in the normoglycemic range and overweight. For these specific subpopulations we can then suggest a more personalized follow-up.

In conclusion, while the current era of statistics and machine learning holds great promise and excitement, it faces significant challenges in various scientific domains, particularly in the biomedical field, due to the inherent high variability in predictive tasks. However, it is crucial not to succumb to pessimism. We advocate for a stronger emphasis on uncertainty quantification as a crucial driver for improving predictive models.

A comprehensive evaluation of uncertainty levels in predictions and the subsequent characterization of the reliability conditions of these models should serve as a valuable guide to identify additional requirements for measurement, particularly in the context of personalized follow-up where the risk of diseases and uncertainty are both high. Recently, there has been ongoing debate surrounding the communication of uncertainty and its varying impacts on individuals and different formats.15

Ultimately, the next significant stride in predictive models within medicine relies not solely on a simplistic competition based on accuracy measurements,16 but rather on the potential insights that lie within the realm of uncertainty. The COVID-19 pandemic confirms this fact, highlighting the limitations of simplistic utilization of systematic statistical models,17,18 and presenting opportunities for uncertainty quantification in different contexts. For example, in the case of seroprevalence estimations in Spain, a new stochastic conformal simulation model provides a more comprehensive understanding of pandemic control.19 Exciting new knowledge awaits discovery within this uncertain landscape, and the revolution of this statistical modeling is already underway.