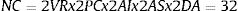Los ensayos clínicos –y también los estudios observacionales aplicados a clínica– están diseñados para responder una o varias preguntas de investigación. La pregunta de investigación lleva implícita una o varias exposiciones (tratamiento, hábito de salud) y uno o varios efectos en salud, que se formulan en forma de hipótesis de investigación. Para contrastar estas hipótesis se diseña un estudio, que al ejecutarlo se obtienen unos datos. En la fase de análisis, esos datos se contrastan con las hipótesis inicialmente planteadas, aplicando las pruebas estadísticas adecuadas según la naturaleza de las variables independientes y dependientes.
Si en el análisis estadístico se observan diferencias en la variable respuesta (según el nivel de la exposición; p. ej. tratamientos), estas pueden deberse a: 1) el efecto real del tratamiento, 2) un sesgo, o/y 3) a un error aleatorizado (azar)1. La estadística nos permite cuantificar qué probabilidades hay de que las diferencias encontradas entre las exposiciones se deban a un error aleatorizado en el proceso de seleccionar la muestra de estudio. Debemos pensar que los sujetos que entran a formar parte del estudio son en realidad una muestra de la población a estudio, y que de esta población se pueden extraer infinitas muestras, que van a ser diferentes entre ellas, y potencialmente distintas a la población. Por tanto, la muestra de nuestro estudio puede diferir aleatoriamente de la población.
Mediante los test de hipótesis, la estadística calcula la probabilidad de que, no existiendo esas diferencias entre los tratamientos en la población, las hayamos encontrado en nuestros datos por azar. Si esta probabilidad es menor que una fijada a priori (riesgo alfa=0,05), podemos concluir con una seguridad del 95% que esta diferencia también existe en la población. Pero con ello estamos admitiendo que nos podemos equivocar una de cada 20 veces concluyendo que existen diferencias en la población, cuando realmente no las hay (falso positivo).
El problemaEl problema surge cuando realizamos múltiples comparaciones no planificadas. Cuantas más comparaciones hagamos, mayor será la probabilidad de encontrar que alguna de ellas sea un falso positivo2. SiNC es el número de comparaciones, la probabilidad de encontrar al menos una asociación estadísticamente significativa por azar es: 1-(0,95)NC. Así, si se realizan 25 comparaciones, la probabilidad de encontrar un falso positivo pasa del 5% al 72%. Y esto puede ser especialmente problemático cuando se hace una publicación selectiva de los resultados estadísticamente significativos,3 ya que la probabilidad de que se deban al azar es cercana a uno.
Principales modos de realizar comparaciones múltiples en estudios clínicosIncluir nuevas variables respuestaLa pregunta de investigación de un ensayo, generalmente, lleva implícita una única variable respuesta principal, pero es muy común que los investigadores analicen otras que no estaban planificadas, sobre todo cuando los resultados con la variable respuesta inicial no es el esperado al plantear la hipótesis. Se buscan otras variables, o se construyen unas nuevas a partir de las existentes para «ver si algo sale estadísticamente significativo». Ello aumenta el riesgo de encontrar falsos positivos.
Para evitarlo, los autores deben evitar incluir variables resultado no planificadas y, si lo hacen, dejar claro que es un análisis post hoc (a posteriori), además de mostrar todas las comparaciones realizadas2. Esto evita realizar una publicación selectiva de los resultados estadísticamente significativos. Para evitar una interpretación sesgada por la publicación selectiva, los lectores, revisores y editores deberían comprobar que las variables resultado estaban contempladas a priori en la metodología y en el registro del ensayo. Existen múltiples registros de ensayos4–6, pero en ocasiones (dependiendo del país y el año de realización) puede ocurrir que el grado de detalle sobre la construcción de las variables resultado sea insuficiente.
También la categorización de las variables respuesta está sujeta a selección oportunista post hoc en función de los resultados más llamativos. Por ello, sería interesante establecer en el protocolo los puntos de corte o usar unos de referencia internacionales ya admitidos7.
Análisis por subgruposA diferencia del análisis por grupos (definido a priori por la pregunta de investigación), en el análisis por subgrupos, estos suelen definirse a posteriori (una vez finalizada la recogida de datos). En el análisis por subgrupos se evalúan los efectos del tratamiento en subpoblaciones de pacientes según características basales clínicas (p. ej. diabetes, gravedad) o personales (sexo, edad, genética). El objetivo es evaluar si los efectos de los tratamientos varían dependiendo de ciertas características de los pacientes.
Existe una controversia sobre si se deben realizar o no8: no hacerlos puede privar de nuevos conocimientos científicos, y realizarlos aumenta la posibilidad de obtener falsos positivos por la utilización de comparaciones múltiples.
Las recomendaciones para tener en cuenta en los análisis por subgrupos son9:
- (1)
En el caso de que el análisis por subgrupos estuviera establecido en el protocolo, y su número sea reducido.
- (2)
Utilizar cálculos de interacciones para valorar la heterogeneidad entre grupos. El nivel de significación estadística de las interacciones permite valorar si el azar puede explicar las diferencias entre los subgrupos.
- (3)
Los resultados son consistentes con otros estudios y son biológicamente plausibles.
Son análisis de datos realizados antes de finalizar el estudio, y tienen por objetivo obtener resultados preliminares que aconsejen interrumpir o no el estudio. Los principales motivos para detener un estudio son que9: 1) se determine que un medicamento es dañino, 2) sea altamente beneficioso, 3) la probabilidad de demostrar eficacia sea insignificante. Esta decisión la debería tomar un comité de seguimiento de datos independiente y no los propios investigadores. En todo caso, es necesario resaltar que aun en este caso, y a pesar de que se corrija el nivel de significación por técnicas estadísticas como O’Brien-Fleming, Peto o Pocock,9 las estimaciones del efecto del tratamiento estarán siempre sesgadas.
Otros aspectos metodológicos que pueden aumentar el error tipo I de un ensayo son cómo tratar los valores ausentes (hay distintos métodos estadísticos para hacerlo), o cómo analizar las pérdidas durante el seguimiento (intención de tratar o por protocolo).
ConclusiónExisten múltiples maneras de hacer comparaciones no planificadas: con distintas variables respuesta, con distintas formas de agruparlas o categorizarlas, con análisis intermedios, realizando análisis por subgrupos, con distintas maneras de abordar los datos ausentes o las pérdidas durante el seguimiento.
Todas estas posibilidades no son aisladas, sino que se pueden dar combinaciones de ellas, lo que hace que las posibilidades de comparaciones no planificadas se multipliquen. Así, en el caso conservador de solo probar dos variables respuesta VR, con dos puntos de corte PC, con un análisis intermedio y uno final AI, y dos análisis por subgrupos AS, probando dos maneras de tratar los datos ausentes DA, el número final de combinaciones es de:
De esta manera, la probabilidad de encontrar un falso positivo asciende del 5% al 81% 1−0.95NC=0.81. Y, si el autor solo muestra en el artículo los «estadísticamente significativos», las probabilidades de que ese hallazgo sea un falso positivo es altísima. Y esto puede ser especialmente grave para la salud pública y en clínica si las decisiones se basan en estos falsos positivos.
Por ello, es especialmente importante que todos los análisis estadísticos estén planificados a priori, y que en los registros de los ensayos se detallen todos los análisis que se van a realizar. Así editores, revisores y lectores pueden cotejar lo publicado con lo planificado, lo que les permitirá valorar hasta qué punto el resultado obtenido se puede deber a un falso positivo.